Símplice

Dados $k + 1$ puntos $v_{0}, \dots, v_{k}$ de $R^{m}$ afínmente independientes^[1], el subconjunto convexo de $R^{m}$ más pequeño que los contiene se conoce como un $k$ -símplice, lo denotaremos por:

σ = [v_{0}, \dots, v_{k}]

Los puntos $v_{i}$ se llaman los vértices del $k$ -símplice. La dimensión de $σ$ es $k$ .

Subsímplices y caras

Si $σ = [v_{0}, \dots, v_{k}]$ es un $k$ -símplice, cualquier subconjunto no vacío de vértices también determina un símplice que llamaremos subsímplice de $σ$ . Si solo se omite un vértice, el subsímplice correspondiente se denomina cara.

Caras de $σ$ :

[v_{0}, \dots, \hat{v_{i}}, \dots, v_{k}]

Ejemplos

Un $0$ -símplice es un punto; un $1$ -símplice es un segmento de línea; un $2$ -símplice un triángulo; y un $3$ -símplice un tetraedro.
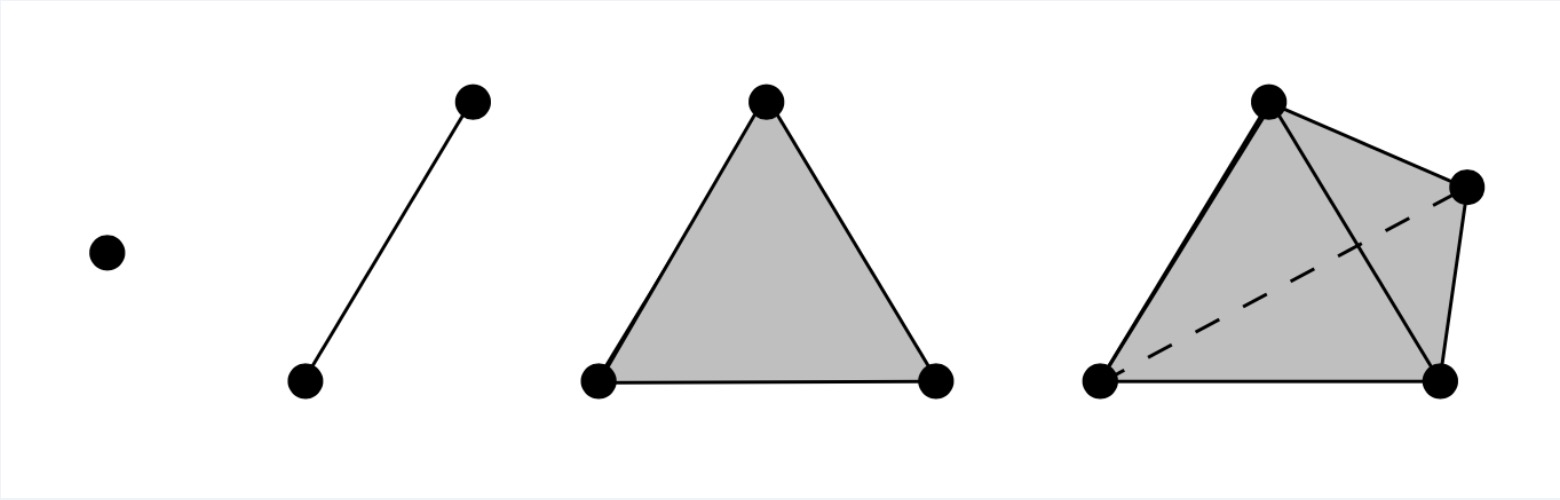
$Pasted image 20250326224112.png$
Por otro lado, las $0$ -caras se llaman vértices; las $1$ -caras son lados o aristas; y las $n - 1$ -caras son facetas o caras, como se ha definido arriba.

Los puntos $v_{0}, v_{1}, \dots, v_{k} \in R^{m}$ son afínmente independientes si el conjunto de vectores de diferencias $v_{1} - v_{0}, v_{2} - v_{0}, \dots, v_{k} - v_{0}$ es linealmente independiente. Es una generalización de la independencia lineal. En este contexto, garantiza que se defina un símplice de la dimensión adecuada, no pudiendo colapsar todos los puntos en un subespacio de menor dimensión (como por ejemplo pasaría si todos los puntos de un triángulo estuvieran alineados). ↩︎